-
分数の加減
-
どうすればいい
6年生に次のような問題やってもいます。
問題1:紐を1m物差しで測ったら半端な長さが残りました。そこでその半端な長さを基にして1mの長さを測り返すと、半端な長さ3つ分でぴったり1mになることが分かりました。半端の長さは分数で表すと何mだと言えますか?
すると、ほとんどの子が1/4mと答えます。正解は1/3mなのですが全体を1と見る(割合分数)で分数を認識するとこういった結果になりがちです。また、同様に次のような問題でも躓く子が多いのです。
もちろん答えは2/3mなのですが、たくさんの子が1/3mと答えます。この事は今から50年前から知られていました。そして50年たった今でも変わっていません。(算数が苦手な子は間違いなくこの問題で躓きます)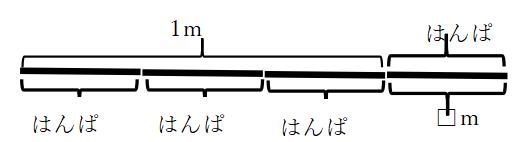
そんなわけで現在の教科書は長さ(1m)を基本にして分数を教えるようになっています。しかし、残念なことに長さは直線でしか表せないため操作したり、思い描いたりする事がしにくいという欠点があります。そこで最近の教科書は<幅を持たせた直線図(テープ図)>を使うようになっています。単なる直線に比べるとテープ図の方がましです。しかし、どうやっても長さは1mごとに切り離して扱うことが出来ないという欠点があり、長さで分数を導入するのはいい方法とは言えないのです。3・4年生の段階では液量をメインの量とした方が長さより分かりがいいのです。液量は容器とセットですから、単位量(1L)を切り離して扱うことが出来ます。その上、面積図をモデルとすることが容易で、操作を通して分数で表された量感がイメージしやすいのです。液量のこういった特性は分数計算の図解や分数の変身・変装(帯分数・仮分数・倍分・約分)の理解に適しています。
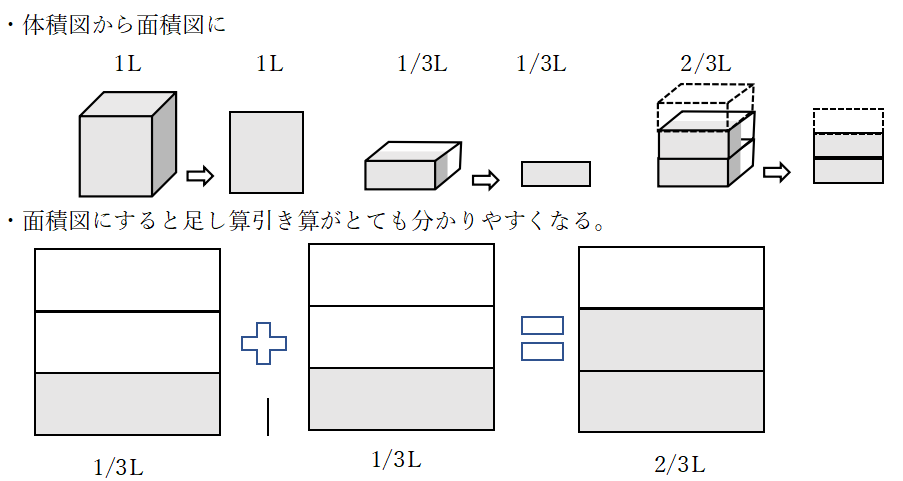
YouTube有
YouTube有
<詳しく知りたい人へ>