-
小数剰除決定のつまずき
-
どうすればいい
5年になって最初に躓くのは小数の乗除です。ここでの躓きは文章問題を読んで、「この問題はかけ算で解くのか、割算で解くのか」が分からなくなるという躓きと、筆算形式になったときの小数点の処理、あるいは割算での端数の処理(小数第2位で四捨五入・小数第1位まで計算してあまりを出す)の躓きがあります。
はじめに演算決定が出来ないと言う問題では多くの子が2年から5年までのかけ算・割算の仕組みが十分に理解できていないという根本的な問題があります。子どもたちの多くはかけ算・割算の文章問題は出来ていたのだけれど、肝心なことが分かっていないままになっていた可能性があるのです。肝心なこととは「何に何を掛けて何を求めているのか?」「何を何で割って何を求めているのか?」というかけ算・割算の仕組みが分かっていないため演算決定が難しく途方に暮れる子が出てきます。
乗除の意味の構造は仕組みは次のようになっています。
「1あたりの量(数)×いくつ分の量(数)=全体の量(数)」
「全体の量(数)÷いくつ分の量(数)=1あたりの量(数)」
「全体の量(数)÷1あたりの量(数)=いくつ分の量(数)」
いろんな文章題がありますが、乗除文章題の単純な問題のほとんどはこの3つの仕組みの中に収まります。この仕組みを理解させるためには問題文をかけわり図に書かせることでかなり分かりやすくなります。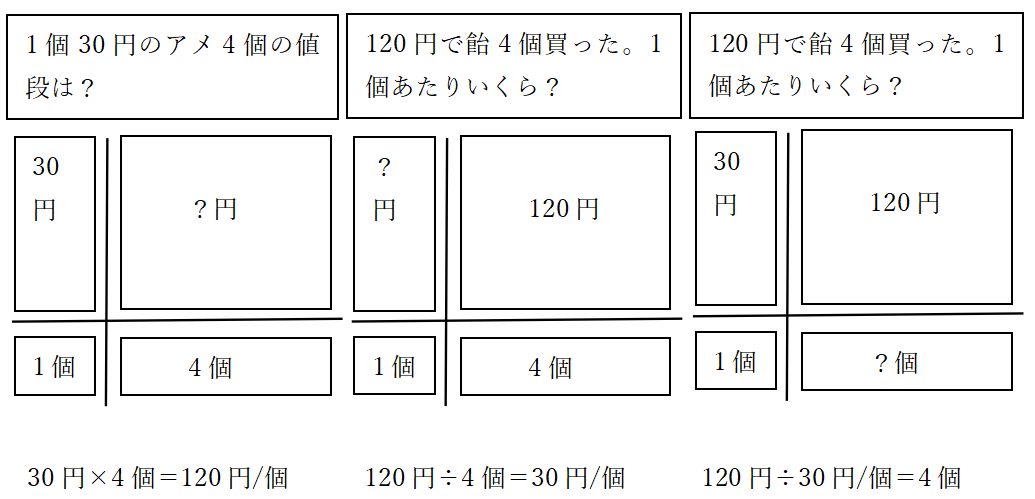
こういった指導が早い時期から行なわれていると小数分数値になっても何を何でどうするのかという理解ができるように思います。
YouTube
<詳しく知りたい人へ>