-
小数わり算ひっさん
-
どうすればいい
小数の割算は小学校算数の一つの鬼門です。まず3桁÷2桁の計算がこなせていない。次に小数では割る事ができないのでたとえば割る数を10倍してを整数にする。その分割られる数も10倍して計算するとよいという理屈があるのですが、この理屈(数理)が分からない子も多いです。その上、小数の端数部分を四捨五入して概数にしたり、割り切れない場合はあまりを出したりなどという結構複雑な端数処理があり、そこでも躓く子が結構います。
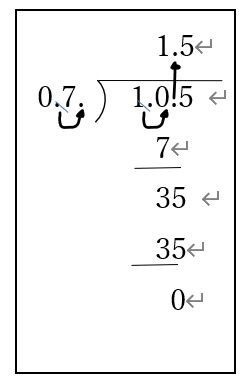
問題、0.7mで1.05kgの棒があります。この棒1mあたりの重さは何kgでしょう?小数の割算では割算は割る数と割られる数に同じ数をかけて答えを出しても答えは同じになるという性質を使って÷小数を÷整数に変換して計算します。
こういった操作は筆算式の小数点を移動させる方式となります。
・0.7を7にするために小数点をひとつ下の位に移動します。その とき曲線矢印を書かせ、もとの小数点を消します。
・次に1.05も同じようにして曲線矢印を書かせ、もとの小数点を 消します。
ここまでが教科書の説明・私はそれに次の事柄をつけくわえます。
・移動した小数点のすぐ上、答えを書くところに小数点を書かせ ておきます。(こうすることで小数点の打ち忘れが防げます)
・この方法を<小数点お皿移し上げの術>と呼ばせます(こういった名前を付けておくと操作を忘れないのです)
☆割り切れないときの概数処理
問題、0.7mで1.03kgの棒があります。この棒1mあたりの重さは何kgでしょう?小数第1位までの概数で答えなさい。
式1.03kg÷0.7m=□
1本の仕切り線で解決します。
・小数点お皿移し上げの術を先にやります。計算を進める前に「小数第1の位までの概数」にすると言うことは「小数第1位の数字より下の数字が端数と見るという事だから仕切り線を入れておこう」と言って小数第1位と第2位の間に線を入れさせます。
・仕切り線の下にまで商を立てさせます。小数第2位まで商がたった場面で計算をやめ{7}は切り上げか切り捨てかを判断させます。
・7つまり0.07を0.1として切り上げ1.4+0.1で1.5になることを確認して1.4の上に約1.5と書き込ませます。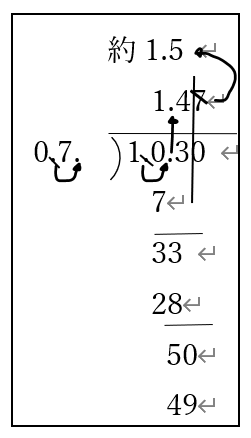
☆割止めあまりだしの計算が分からない
割り切れないであまりを出さないといけない場合があります。例えば 3.85mのロープから1.8mの縄跳ロープは何本作れて、何mあまりますか?という問題などの場合がそれに当たります。
できるだけ具体的な問題を実際にやってみる
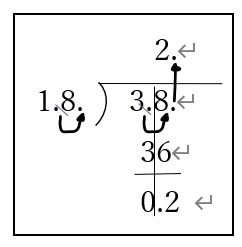
式3.8÷1.8=□あまり( m)
計算で出てくる答えは2あまり2です。この答えに単位を付けさせ ます。答えの2は2本です。「あまりの2は果たして2mかな?」 と問いかけてください
もともとは3.8mの中に1.8mが何本取れるのかと言う問題でした。従ってあまりは0.2mのはずです。計算では38÷18=2あまり2となっています。これは3.8mは0.1mが38個、1.8mは0.1mが18個あると考えて38個÷18個の計算をしているのです。従ってあまりの2も実は0.1mが2個なので実際の量で表すと0.1m×2=0.2mという事になるのです。でもいちいち0.1が2個だからと考えるのは面倒です。そこである技があります。それは<小数元点下ろしの術>です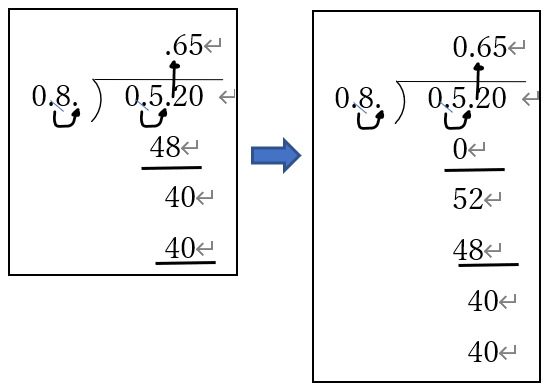
・38÷18の計算が終わった後、もともとの小数点のあった位置に区切り線を入れてください。 ・もとの小数点をあまりの数の前に下ろしてきて0.を書き加えます。
YouTube有
<詳しく知りたい人へ>